サスペンションとはなにか 第4回 サスペンションの決定的真相は「自由度の法則」だ:その3[自由度の計算の仕方:軸による拘束]
- 2021/06/29
-
福野礼一郎


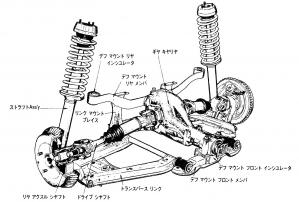
今回は独立懸架式サスとしてはもっともよく知られたダブルウィッシュボーン式を計算してみます。
TEXT:福野礼一郎(FUKUNO Reiichiro)
第2回 サスペンションの決定的真相は『自由度の法則』だ:その1では5リンク式マルチリンクの自由度を計算しました。
サスの構成要素がそれぞれ持っている運動の6自由度から、ピンジョイントによって拘束されている自由度と、サスにとって無意味な自由度を引いていくと、残り自由度が「1」になって、独立懸架式サスペンションとは「タイヤに1自由度(の運動)を許容するリンク機構」であるという定義が成立することが立証されました。
今回は独立懸架式サスとしてはもっともよく知られたダブルウィッシュボーン式を計算してみます。
ダブルウィッシュボーン式とは
ダブルウィッシュボーン式というのは、A型をしたアーム→Aアームでアッパーアームとロワアームを構成したサスです。第2回 サスペンションの決定的真相は「自由度の法則」だ:その1で解説したように、このAアームは2本のリンクのハブ側の取り付け点くっつけて共用することで、2本のアームをAアームへと簡略化した形式、とみなすことができます。したがってダブルウィッシュボーンは5リンク式マルチリンクの簡略形と考えることができます。

第2回 サスペンションの決定的真相は「自由度の法則」だ:その1[5リンク式マルチリンクは独立懸架サスの基本だ]
なぜサスにはあんなにたくさんあれこれいろんな形式があるのでしょう。 TEXT:福野礼一郎(FUKUNO Reiichiro)
余談ですが「ウィッシュボーン」とは鳥の胸骨のことで、実際の骨はY字型をしています。
感謝祭やクリスマスに七面鳥を丸焼きにしてみんなで食べていると、お肉のなかからこのY字型をした細い骨が出てきます。そしたら有志2名がそれぞれY字型の角の部分を指で持ち、願い事をしてから引っ張りあいます。どちらかの端がぽきっと折れ、片方の人にY字の縦棒が残ると願いがかなうという遊びです。それで「願いをかける骨=ウィッシュボーン」といいます。
ダブルウィッシュボーン式にもいろいろありますが、まずこれ。さっきの図と同じです。50~80年代のアメリカ車やスーパーカーがフロントサスに使っていたもっとも古典的なタイプです。

手前に1本リンクがついているのは、フロントサスの場合に操舵をおこなうタイロッドです。
タイロッドは通常サスアームとしては考えられていないかもしれませんが、タイヤと車体を結び、サスが上下に動いたときのタイヤのトー方向(=操舵方向)の向きの変化(=アライメント変化)に影響を与えていますから、立派にサスのリンク機構の一員です。
ちなみにこのサス形式をリヤに使っている場合、フロントサスでいうタイロッドはトー方向の動きを規制するトーコントロールリンクに置き換わります。リヤサスに4WS機構(後輪操舵機構)がついている場合は、トーコントロールリンクがそのままアクチュエーターに置き換えられていることが多いです。
ではこのサスの自由度を計算してみましょう。サスペンションに出会ったらまず自由度の計算です。
ダブルウィッシュボーン式の自由度の計算
①サスの構成要素から総自由度を算出する
サスの構成要素をかぞえ、それに6自由度をかけてサスの総自由度を出します。
詳しくは第3回 サスペンションの決定的真相は「自由度の法則」だ:その2の5リンク式マルチリンクの計算を参照してください。

第3回 サスペンションの決定的真相は「自由度の法則」だ:その2[自由度の計算の仕方:ピンジョイントの拘束]
連載「サスペンションとはなにか」の第3回、テーマは自由度の計算の仕方:ピンジョイントの拘束です。 TEXT:福野礼一郎(F...
このサスの場合、構成要素はタイヤ+ホイール+ハブで1つ、アッパーアームで1つ、ロワアームで1つ、タイロッド(またはトーコントロールリンク)で1つ、合計4つです。
構成要素が5リンク式マルチリンクより2つ減りましたが、2本のリンクの先端をそれぞれくっつけて2本のリンクを1本のAアームに変えたのですから、構成要素が減ったのは当然です。
4つの構成要素がそれぞれ6自由度を持っているので、総自由度は24ですね。
「構成要素:4(総自由度24) 」
②ピン支持部分では「3自由度」を引く
このサスでは、図で黄色い丸で描いている部分がゴムブッシュ→ピンジョイントです。
ピンジョイントでは「6自由度のうちX、Y、Zの並進運動を拘束し、X軸、Y軸、Z軸周りの回転運動は許容している」と考えるんでした(→第3回 サスペンションの決定的真相は「自由度の法則」だ:その2)。

第3回 サスペンションの決定的真相は「自由度の法則」だ:その2[自由度の計算の仕方:ピンジョイントの拘束]
連載「サスペンションとはなにか」の第3回、テーマは自由度の計算の仕方:ピンジョイントの拘束です。 TEXT:福野礼一郎(F...
この場合ピンジョイントは4ヶ所。3×4ヶ所=12を総自由度24から引きます。
残りの自由度は12です。
構成要素:4(総自由度24)-ピン拘束「-3」×4ヶ所=残り自由度12
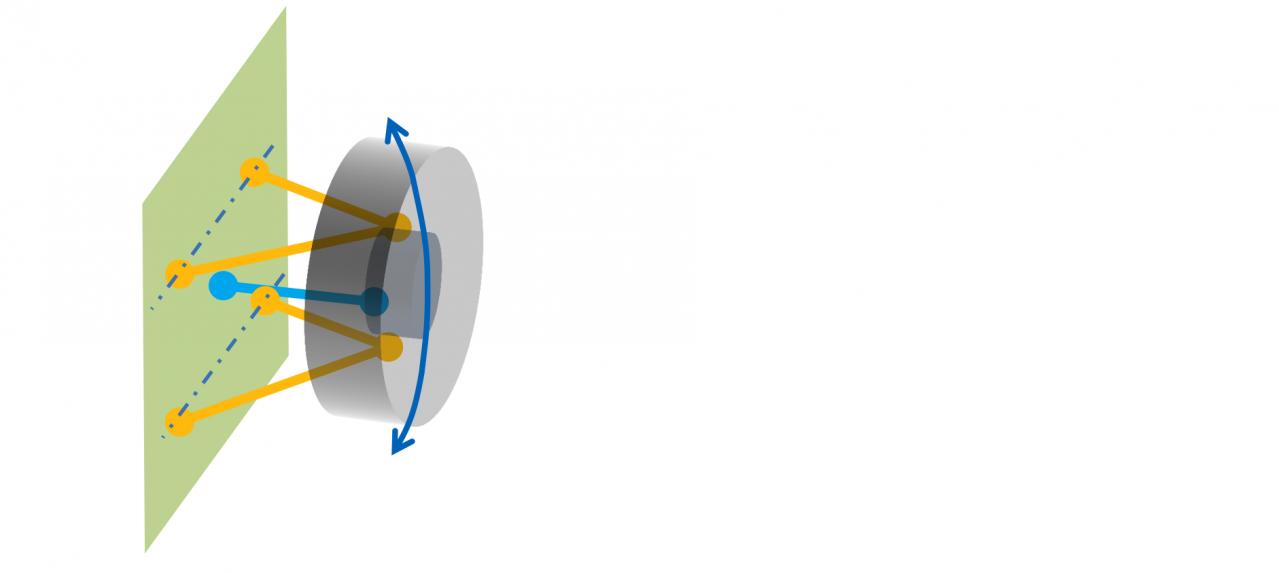
③軸支持部分では「5自由度」を引く
このサスでは上下のAアームのボディ側の取り付け部はピンジョイントではなく回転軸受けになっています。図でもちゃんと軸っぽく描いてあります。
「軸支持」というのは物体の6自由度の運動のうち「X、Y、Zの並進運動のすべてを拘束するだけではなく、X軸、Y軸、Z軸周りの回転運動のうちの2つも拘束し、1軸周りの回転運動だけを許容する」という支持方式です。
つまり軸支持は5自由度を拘束して奪うということですね。
というわけで、サスの構成要素の中にもし軸支持部位があれば、1ヶ所につき「5自由度」をサスの総自由度から引きます。
軸支持は2ヶ所=10自由度拘束ですから、それを奪うと残りは2自由度になりました。
構成要素:4(総自由度24) ピン拘束「-3」×4ヶ所 軸拘束「-5」×2ヶ所 残り自由度2
④リンクの回転運動を引く
忘れがちになるアレです。リンクの両端がピンジョイントの場合、リンクはその場でシャフトのように回転することができますが、この自由度はサスの作動には直接関係がないので、無視して引くんでした。
ここではタイロッド(またはトーコントロールリンク)がそれです。
残り自由度2から1自由度を引くと.......残自由度はみごとに1となって、独立懸架式サスが成立しました。
........すごくないですか? 私は最初これを計算してみたとき、ついにサスペンションの秘密を知った気がして感動しました。

ダブルウィッシュボーン式サスの自由度
構成要素:4(総自由度24)、ピン拘束「-3」×4ヶ所 軸拘束「ー5」×2ヶ所 軸回転-1 残自由度「1」
① 自由度の計算:サスの構成部材がもつすべての自由度から、拘束した自由度と無用な自由度を引く
② フロントサスのタイロッドはリヤサスのトーコントロールリンクと同様、サスのリンクである
③ 軸支持は5自由度を拘束する
④ 独立懸架式サスペンションでは①の計算の残りの自由度は原則「1」になる
⑤ 独立懸架式サスペンションとは「タイヤに1自由度(の運動)を許容するリンク機構」である
|
|
|

自動車業界の最新情報をお届けします!
Follow @MotorFanwebおすすめのバックナンバー
これが本当の実燃費だ!ステージごとにみっちり計測してみました。

日産キックス600km試乗インプレ:80km/h以上の速度域では燃費が劇...

BMW320d ディーゼルの真骨頂! 1000km一気に走破 東京〜山形往復...

日産ノート | カッコイイだけじゃない! 燃費も走りも格段に洗練...

渋滞もなんのその! スイスポの本気度はサンデードライブでこそ光...

PHEVとディーゼルで燃費はどう違う? プジョー3008HYBRID4とリフ...

スズキ・ジムニーとジムニーシエラでダート走行の燃費を計ってみた...
会員必読記事|MotorFan Tech 厳選コンテンツ

フェアレディZ432の真実 名車再考 日産フェアレディZ432 Chapter2...

マツダ ロータリーエンジン 13B-RENESISに至る技術課題と改善手法...

マツダSKYACTIV-X:常識破りのブレークスルー。ガソリンエンジン...

ターボエンジンに過給ラグが生じるわけ——普段は自然吸気状態

林義正先生、「トルクと馬力」って何が違うんですか、教えてくだ...

マツダ×トヨタのSKYACTIV-HYBRIDとはどのようなパワートレインだ...
3分でわかる! クルマとバイクのテクノロジー超簡単解説

3分でわかる! スーパーカブのエンジンが壊れない理由……のひとつ...

3分でわかる! マツダのSKYACTIV-X(スカイアクティブ-X)ってな...

スーパーカブとクロスカブの運転が楽しいのは自動遠心クラッチ付...

ホンダCB1100の並列4気筒にはなぜV8のようなドロドロ感があるのか...

ホンダ・シビック タイプRの謎、4気筒なのになぜマフラーが3本?